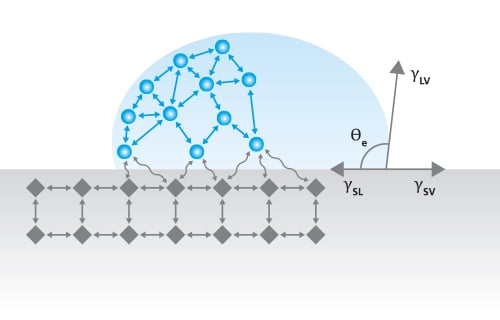
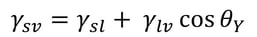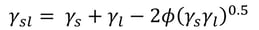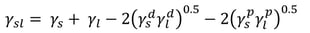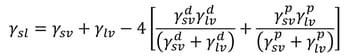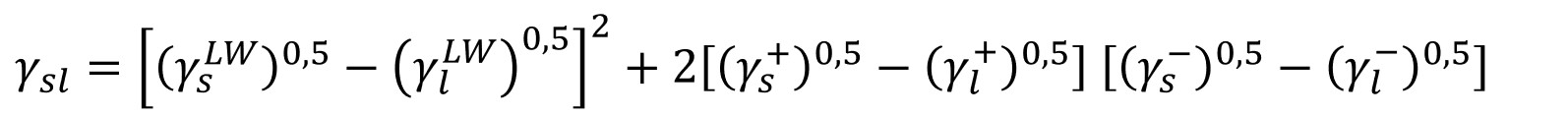Most of the surface free energy theories have a basis in the understanding of the molecular interactions at the liquid-solid interface.
Young’s equation states
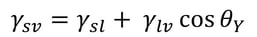
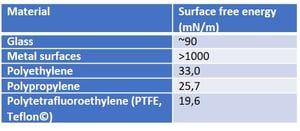
, where γsv is the surface free energy, γsl is the interfacial tension between the liquid and the solid, γlv is the surface tension of the liquid, and θY is the contact angle on a surface. Out of these, the surface tension of the liquid and the contact angle can be easily measured. The interfacial tension between the solid and the liquid is the property that has caused a lot of debate during the last two centuries.
At the moment, the most used interfacial tension relationship is based on that presented by Girifalco and Good.
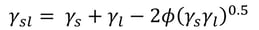
, where φ = 1 is assumed. This is the basis of the most used SFE theories still today.
Owen, Wendt, Rabel and Kaelble (OWRK) method
OWRK is the most used surface free energy method. It separates the interactions at the liquid-solid interface into dispersive and polar. The idea that the quantity of the interfacial tension is determined by various interfacial interactions that depend on the properties of both the measuring liquid and the solid surface was presented by Fowkes. He assumed that the surface free energy of a solid and surface tension of a liquid is a sum of independent interactions such as dispersion, polar, hydrogen (related to hydrogen bonds), induction, and acid-base components. In OWRK method, the multicomponent approach is accepted but the interactions are divided into dispersive and polar, only. The polar interactions contain then all the other interactions (except the dispersive) mentioned above.
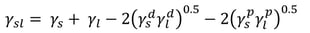
Wu method
Wu agreed with Owen et al. and divided surface free energy into dispersive and polar components. He, however, used a harmonic mean of the interfacial interactions instead of a geometric one. The interfacial tension could then be written as
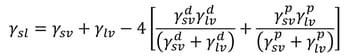
Van Oss - Chaudhury - Good (vOCG) theory
The newest theory was developed by Van Oss, Chaudhury, and Good. They divided the interactions into the long-range interactions which include London, Keesom, and Debye interactions. This component is called the Lifshitz-van der Waals component (γLW) and is equivalent to the dispersive part of the OWRK theory. The other part contains short-range interactions called the acid-base component (γAB) which is divided into acidic (γ+) and basic (γ-) constitutes.
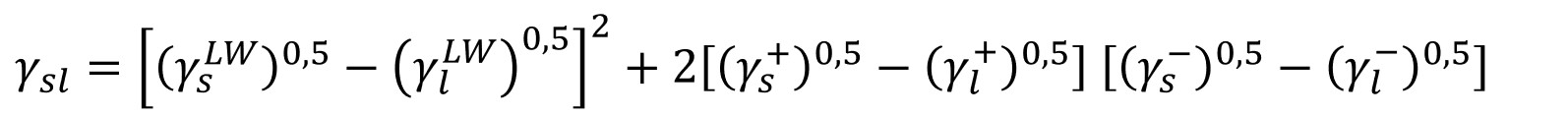
This theory, sometimes also called acid-base theory is the second most used surface free energy theory. It has especially been utilized to look at interactions of proteins (and other biopolymers) with hydrophobic solids.