Contact angle and surface roughness

Both chemical and topographical properties of the surface are important parameters in many different applications and processes, where wetting and adhesion behavior needs to be optimized. Wettability can be studied by measuring the contact angle of the substrate with the given liquid. The well-known Young equation describes the balance at the three-phase contact of solid, liquid and vapor.

γ_sv = γ_sl + γ_lv · cos θ_Y

The interfacial tensions, γ_sv, γ_sl and γ_lv, form the equilibrium contact angle of wetting, often referred to as the Young contact angle θ_Y. The Young equation assumes that the surface is chemically homogenous and topographically smooth. This is however not true in the case of real surfaces, which instead of having one equilibrium contact angle value exhibit a range of contact angles between the advancing and receding ones.

The figure shows the droplet on ideal and real surfaces. On an ideal surface, the Young equation applies and the measured contact angle is equal to the Young contact angle (upper image). On a real surface the actual contact angle is the angle between the tangent to the liquid-vapor interface and the actual, local surface of the solid (lower image). However, the measured (apparent) contact angle is the angle between the tangent to the liquid-vapor interface and the line that represents the apparent solid surface, as seen macroscopically. Actual and apparent contact angle values can deviate substantially from each other. To calculate real surface free energies of the solid the actual contact angles should be used.

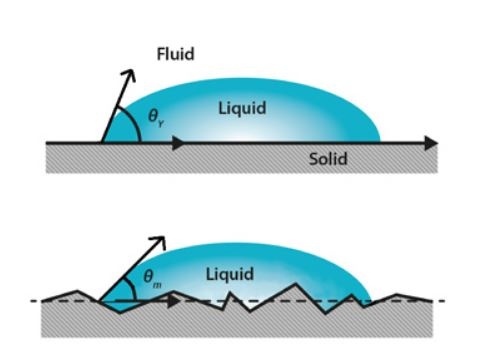Contact angles and surface roughness.

The relationship between roughness and wettability was defined in 1936 by Wenzel, who stated that adding surface roughness would enhance the wettability caused by the chemistry of the surface³. For example, if the surface is chemically hydrophobic, it will become even more hydrophobic when surface roughness is added. Wenzel statement can be described with equation below.

cos θ_m = r · cos θ_Y

Where θ_m is the measured contact angle, θ_Y is the Young contact angle and r is the roughness ratio. The roughness ratio is defined as the ratio between the actual and projected solid surface area (r = 1 for a smooth surface and r > 1 for a rough one) and can be calculated from a 3D roughness parameter S_dr as shown already. It is important to notice that the Wenzel equation is based on the assumption that the liquid penetrates into the roughness grooves (as in Figure 1). It has been stated that if the droplet is larger than the roughness scale by two to three orders of magnitude, the Wenzel equation applies⁴. Wenzel corrected contact angles have been utilized for example to study the wettability of paper sheets⁵ and cell adhesion to biomaterial surfaces⁶. Both micro and nanoscale roughness have been shown to have influence on surface wettability.

For additional information on applications, see:

Application Note 16 — Adhesion to Wood-Plastic Composites

Application Note 17 — Influence of Topography and Wettability on Biocompatibility

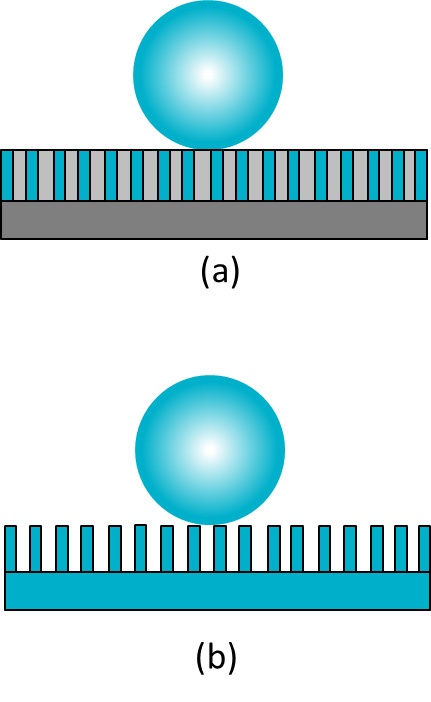
In cases where the liquid does not penetrate into the grooves, the Wenzel equation does not apply. In this case the Cassie equation is used instead. The Cassie equation was first developed to describe chemically heterogeneous surfaces, with two different chemistries⁷.

cos θ_m  = x₁ · cos θ_Y1 + x₂ · cos θ_Y2

In the equation above, x is the area fraction characterized by the given chemistry and subscripts 1 and 2 indicate two different surface chemistries (Figure a). If, instead of having different chemistries on the surface, the second area is air like (Figure b), then equation can be written as,

cos θ_m  = x₁(cos θ_Y + 1) – 1

Since contact angle against liquid and air can be considered to be 180° (cos θ_Y2 is -1) and the area fraction x₂ = 1 – x₁. This equation was developed by Cassie and Baxter⁷ and is thus often called the Cassie-Baxter equation. It has been found that for the droplet to achieve the real Cassie-Baxter stage (no penetration of the liquid inside the grooves), the geometry of the roughness has to be carefully designed⁸.

The most stable contact angle is the one associated with the absolute minimum of the Gibbs energy curve, which can be connected to Young’s contact angle. The contact angles calculated from the Wenzel and Cassie-Baxter equations have been found to be good approximations of the most stable contact angles⁹. 

Roughness parameters

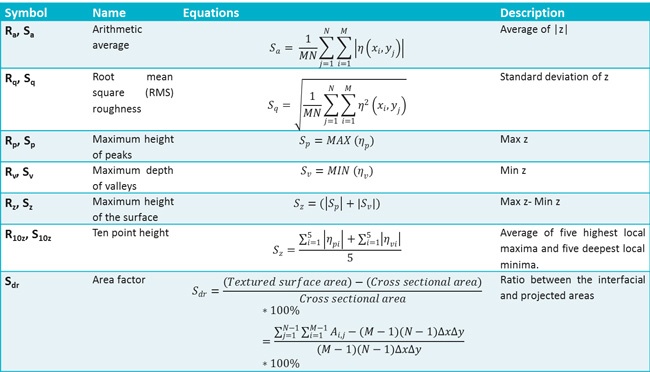
Surface roughness is a measurement of surface texture. It is defined as a vertical deviation of a real surface from its ideally smooth form. Roughness plays an important role in various processes such as friction and adhesion and is widely measured. Surface roughness cannot be accurately characterized by using a single parameter. Instead, a set of surface roughness parameters is defined. Parameters that characterize surface profiles are called 2D parameters and are marked with the letter ‘R’. These parameters are widely utilized in different applica­tions but are not really able to provide the full information on the three-dimensional surfaces. Parameters to characterize surface topography are called 3D parameters and are marked with the letter ‘S’. Some of the 3D parameters have their 2D counterparts; others are specifically developed for 3D surfaces¹. A summary of these parameters as stated by the ISO 25178 (and their 2D counterparts) is presented in table below^{2, ISO 25178}. S_a is an arithmetic mean height of the surface. S_q and its 2D counterpart are the most widely used roughness parameters that give the standard deviation of height. R_p and R_v give the maximum height of the summit and maximum depth of the valleys, respectively. R_z gives the peak-to-peak value and R_10z is calculated as a mean height value of five local maxima and local minima. R_z is more sensitive to noise than R_10z. The ratio between the interfacial and projected area S_dr gives the additional surface area contributed by the texture. This parameter is especially useful in wettability studies since it can be used to calculate the roughness ratio r, according to equation below.

r = 1 + S_dr ⁄ 100