Contact angle, θ (theta), is a quantitative measure of wetting of a solid by a liquid. The contact angle is geometrically defined as the angle formed by a liquid at the three-phase boundary where a liquid, gas, and solid intersect. There are three different forces acting on this three-phase contact point between solid, liquid and gas, or in some cases solid, liquid and liquid. Contact angles can be divided into static, dynamic and roughness corrected contact angle.
Static contact angle
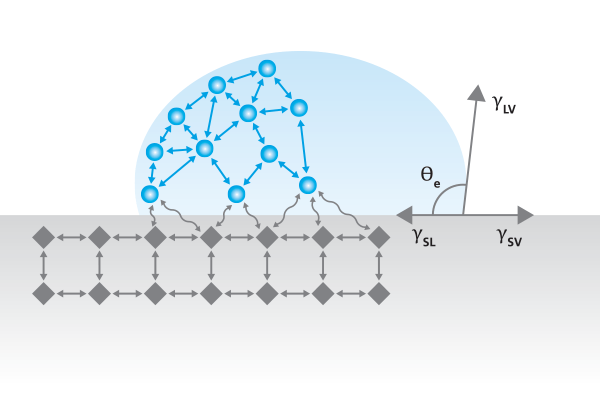
Static (i.e. sessile drop) contact angles are measured when the droplet is sitting on the surface and the three-phase boundary is not moving. Static contact angles are by far the most measured wettability values. It is most suitable for relatively smooth and homogenous surfaces. Static contact angles are also used to define the surface free energy (i.e. surface tension of solid) of the substrate. Static contact angle offers a quick, easy and quantitative measurement of wettability. Static contact angle measurement is based on Young’s equation which assumes that interfacial forces are thermodynamically stable.
Dynamic contact angle, contact angle hysteresis and roll-off angle
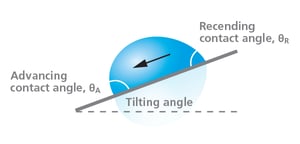
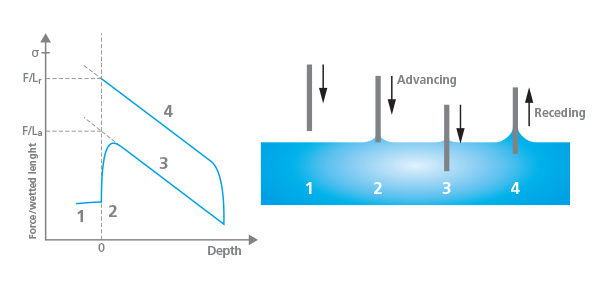
When the three-phase boundary is moving, dynamic contact angles can be measured, and are referred to as advancing and receding angles. As the terms imply, advancing contact angle is measured when the droplet front is advancing and receding when the droplet front is receding. On an ideal surface, these two values are close to each other. However, most often, the measured contact angle depends on the direction on which the contact line is moving. Contact angle hysteresis is the difference between the advancing and the receding contact angles. Contact angle hysteresis arises mostly from the chemical and topographical heterogeneity of the surface, solution impurities absorbing on the surface, or swelling, rearrangement or alteration of the surface by the solvent.
The roll-off angle refers to a tilting angle at which the droplet starts to move. A low roll of angle is related to low contact angle hysteresis.
Roughness corrected contact angles
Contact angles are affected by roughness. Surfaces with the same chemical composition but different roughness will have different contact angles. Roughness corrected contact angles are contact angle values where the effect of roughness is taken away. Roughness corrected contact angles should especially be used when surface free energies are determined.




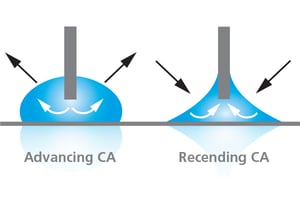 In the
In the