Both chemical and topographical properties of the surface are important parameters in many different applications and processes, where wetting and adhesion behavior needs to be optimized. Wettability can be studied by measuring the contact angle of the substrate with a given liquid. The Young equation describes the balance at the three-phase line between solid, liquid and gas:
γsv = γsl + γlvcosΘY
The interfacial tensions, γsv, γsl and γlv, form the equilibrium contact angle of wetting, referred to Young’s contact angle ΘY. Young’s equation assumes that the surface is chemically homogenous and topographically smooth. This is, however, usually not true in the case of real surfaces, which instead of having one equilibrium contact angle value generally exhibit a range of contact angles between the advancing and receding values.
On the ideal surface, Young’s equation applies, and the measured contact angle is equal to Young’s contact angle (picture on the top).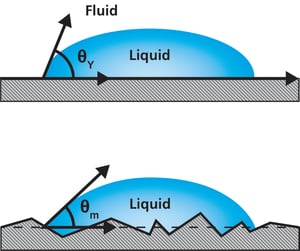 
On a real surface, the actual contact angle is the angle between the tangent to the liquid-fluid interface and the actual, local surface of the solid (picture on the bottom). However, the measured (apparent) contact angle is the angle between the tangent to the liquid-fluid interface and the line that represents the apparent solid surface, as seen macroscopically. Actual and apparent contact angle values can deviate substantially from each other. To calculate theoretically valid surface free energies of the solid the actual contact angles should be used.
The relationship between roughness and wettability was defined in 1936 by Wenzel who stated that adding surface roughness will enhance the wettability caused by the chemistry of the surface. For example, if the surface is chemically hydrophobic, it will become even more hydrophobic when surface roughness is applied. Wenzel’s statement can be described by:
cosΘm = rcosΘY
where Θm is the measured contact angle, ΘY is Young’s contact angle and r is the roughness ratio. Roughness ratio is defined as the ratio between the actual and projected solid surface area (r=1 for a smooth surface and > 1 for a rough surface). It is important to note that the Wenzel equation is based on the assumption that the liquid completely penetrates the roughness grooves. Wenzel equation is an approximation that becomes more accurate as the drop becomes larger compared to the scale of the roughness. It follows that if the drop is larger than the roughness scale by two to three orders of magnitude, the Wenzel equation applies.
To read how Wenzel equation can be applied to obtain roughness corrected contact angles, please download the white paper below.
Susanna is an Application Scientist at Biolin Scientific. In her PhD thesis, she developed fabrication methods for a new type of inorganic-organic polymers. Microfabricated polymer chips were utilized as tool for biomolecule separation in analytical chemistry.
