If you have read a couple of QCM specifications, you may have noticed that the sensitivity parameter is always specified. What is rarely specified, however, is the detection limit. Does it matter? Read on and you will find out. (Spoiler: Yes it does!)
The term ‘sensitivity’ is often mistaken for the smallest quantity that can be usefully detected by the instrument, i.e., the detection limit. In the case of a QCM measurement*, the sensitivity, s, is just a conversion factor used to calculate how much surface mass, Δm, has been added (or removed) given a measured frequency shift, Δf. That is:
Δf = -s x Δm
(The minus sign is there since Δf is negative for a positive mass addition.) For a QCM instrument with a large sensitivity, a given mass change causes a larger frequency shift compared to an instrument with a smaller sensitivity.
So why is not a large sensitivity better than a smaller one? You want to measure a small mass and therefore you want a large signal since a large signal is easier to detect, right? Not so fast. Detection limit is about how large part of the measured signal is useful, not how large the total signal is.
A quick digression. Imagine you are an MD, and you are considering buying one of two digital fever thermometers; one that measures in Fahrenheit and the other in Celsius. You test them to take the temperature of a patient and they show 101.2 F and 38.3 C, respectively. Which one should you buy? Because 101.2 is a larger value than 38.3, does that mean that the Fahrenheit thermometer is better? (Maybe you should ditch both and get one that measures in Kelvin?) Of course not, you want a thermometer that most accurately measures the patient’s temperature, not the magnitude of the value. You can easily convert between Celsius and Fahrenheit (or at least use Google to do it for you). Say that you subject your poor patient to hundreds of repeats, and you notice that the spread in values for the Fahrenheit thermometer is ±0.5 F and ±0.1 C for the Celsius one. Now you can make an informed decision and you should obviously go for the latter (hoping the ethics committee lets you keep your license to practice).
So, back to QCM instruments. An important factor that limits the usefulness of a measured value is frequency noise. This frequency noise has an unfortunate tendency to scale with the sensitivity of the instrument.
The smallest quantity that can be detected with confidence, i.e., the detection limit, is limited by the signal-to-noise ratio, SNR. Noise will be present in all measurements, and it will prevent signals smaller than or comparable to the noise level to be confidently measured.
To detect a signal with confidence, it must be significantly larger than the noise. Typically, a SNR of 2 or 3 is acceptable. For example, if the noise level in your QCM measurement is 0.05 Hz and you accept a signal-to-noise ratio of 2, the detection limit will be 0.1 Hz.
So, will not a higher sensitivity improve the SNR and thereby also improve the performance of the instrument? Not so simple. A higher sensitivity does not by itself provide any advantage, it must be related to the noise, and the noise may increase with the sensitivity. For example, it is well known that QCM sensors with higher fundamental resonant frequency shows a higher sensitivity, but these setups often also show higher noise levels. As a result, the SNR, and the instrument performance, could be the same for two instruments with different sensitivities. This is exemplified in the figure below, where the sensitivity of setup B is four times higher than that of setup A. For the same load, the signal is four times larger in B than in A. However, the noise is also four times higher, which means that the SNR is the same for A and B.
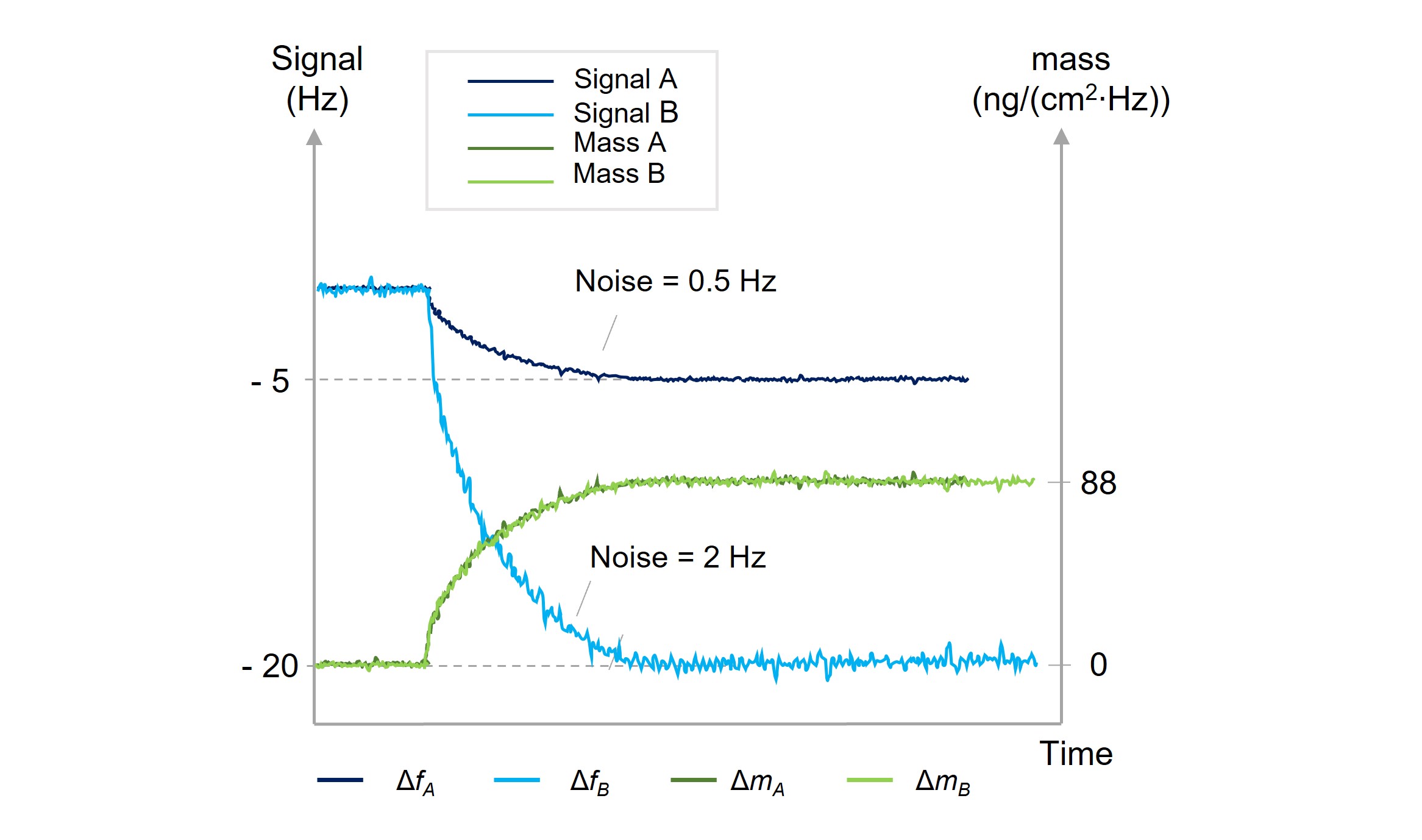
Schematic illustration of two QCM measurements where two hypothetical instruments A and B with different sensitivities and different noise levels were used. The sensitivity of instrument A is four times the sensitivity instrument B, i.e., when the same amount of mass is deposited at the sensor surface, the magnitude of the signal from B is four times the magnitude of the signal from A. As the noise in B is also four times higher than A, however, both A and B show a signal-to-noise ratio of 10. Converting the measured responses to mass, the quantified results from instruments A and B are very similar, which illustrates that the four times higher sensitivity in A is of no use.
Reading a QCM specification you will most surely find the sensitivity specified but it is important to remember that sensitivity is not the same as detection limit. The sensitivity alone will not tell you how small quantities that the QCM instrument in question can usefully detect. The detection limit is determined by the signal-to-noise ratio so when evaluating the performance of an instrument you need to know both the noise level and the sensitivity factor.
Read more about the QCM sensitivity and other parameters found in typical QCM specifications in our guide
*For simplicity, we assume we can use the Sauerbrey equation for converting frequency shift into mass per surface area.
Dr. Michael Rodal is a former employee at Biolin Scientific and a guest writer on the blog. Michael did his Ph.D. in engineering physics and is one of the inventors of the QCM-D technology as well as co-founder of Q-Sense AB. Having developed, and worked with, the technology since the ’90s, Michael is one of the world's leading QCM-D experts.
