If you are familiar with Quartz Crystal Microbalance (QCM) technology, you have most likely also encountered the Sauerbrey equation. This fundamental equation is pivotal for calculating mass changes in thin layers. But what exactly is the Sauerbrey equation, and when should it be applied?
The ability of QCM technology to measure mass changes originates in the discovery of the relation between the resonance frequency and the mass. The relation was formulated in an equation in 1959 by Günter Sauerbrey, at the time a Ph.D. student in Berlin. The equation establishes a linear relationship between the resonance frequency of an oscillating quartz crystal and mass changes. This relationship is expressed in Eq. 1.

where
In practice, this equation is used to determine the mass of thin layers added to a QCM crystal surface. By measuring the frequency change ∆f resulting from the layer addition, the mass ∆m can be calculated.
In this context, it is also worth mentioning that the, the mass sensitivity constant, C, is related to the properties of quartz. For example, for a 5 MHz crystal, C equals 17.7 ng/(cm2∙ Hz).
The Sauerbrey equation is applicable under specific conditions: the added layer must be thin, rigid, and firmly attached to the crystal surface.
The linear frequency-mass relation described by eq. 1, is based on the behavior of a pure quartz crystal, where a crystal of thickness h (and mass m) will have a certain resonance frequency, f (Fig. 1, left).If similar enough to a “pure-quartz” scenario, the scenario where a layer of material, different from quartz, is added to the surface, can be approximated with a thicker crystal.
The model assumes that the added layer can be approximated to be a part of the oscillating crystal itself, which means that the crystal will now have the thickness h + Δh (Fig. 1, right). For this assumption to be valid, the layer on the sensor must be thin, rigid and firmly attached to the crystal surface, and the equation should only be used when these conditions are fulfilled.
If the layer is soft, thick, or not well-coupled to the surface, however, the equation becomes invalid, leading to an underestimation of mass. In such cases, alternative models, such as viscoelastic models, should be considered.
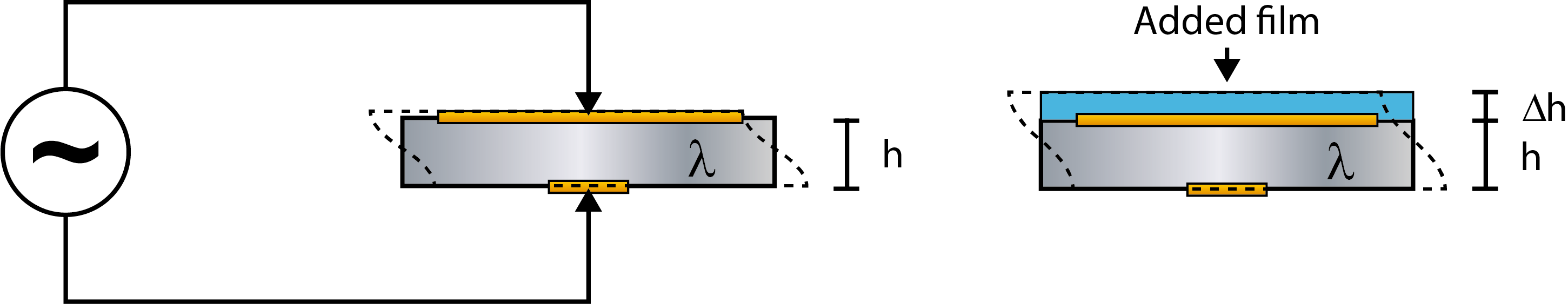 Figure 1. (Left) Schematic illustration of a quartz crystal, of thickness h and mass m, excited to resonance by the application of an alternating voltage.
Figure 1. (Left) Schematic illustration of a quartz crystal, of thickness h and mass m, excited to resonance by the application of an alternating voltage.
(Right) An oscillating crystal with added mass. Now the thickness is h + Δh and the mass is m + Δm.
If you are using a QCM setup that measures the energy loss, e.g. QCM-D, or a setup that has the capability of measuring at multiple harmonics, the applicability of the Sauerbrey equation can be identified by looking at the raw data. The raw data canl indicate applicability, where low energy loss or overlapping overtones suggest that the equation is suitable. . If the Sauerbrey equation is not applicable, then you need to use a model that better describes your layer, perhaps a viscoelastic model, for layer characterization.
Download the overview to learn more about how the Sauerbrey equation is derived and what the different parameters mean.
Editors note: This post was originally published in 2018 and has been updated for comprehensiveness
Compared to QCM, QCM-D measures an additional parameter, and provides more information about the system under study.
Learn about QCM-D, Quartz Crystal Microbalance with Dissipation monitoring - an analytical tool for surface interaction studies at the nanoscale.
Learn about of the acoustic technology, QCM-D, via musical instrument analogies.
Here we explain how Quartz Crystal Microbalance with Dissipation monitoring, QCM-D, works.
Read about how and the QCM fundamental frequency matters in measurements
Read about why it is important for the mass distribution on the QCM sensor to be even, and what the consequences are if it is not.
At first glance, SPR and QCM-D are quite similar. Learn about the key differences and when to use which method
