Bone, wood, and quartz are all piezoelectric materials. But what is piezoelectricity and how does it work? Here we explain where this remarkable property comes from.
Piezoelectricity is a phenomenon which means that there is a coupling between the electrical and the mechanical state of the material. When a piece of piezoelectric material is mechanically deformed, e.g. compressed, a current will flow and charge its faces. And vice versa, the material will be deformed when exerted to an electrical field.
The phenomenon was discovered in 1880 by Paul-Jacques Curie, and his younger brother, Pierre, husband of the well-known Marie Curie. In addition to the materials already mentioned, many more materials exhibit piezoelectric properties, for example, sucrose, silk, Rochelle salt, PVDF, and many ceramics. But why don’t all materials exhibit this property? The reason for that is that for piezoelectricity to appear, the material must be crystalline but not have a symmetry center. Why, we shall soon see.
The manifestation of the pressure-induced current has its origin in the rearrangement of charges within the material. In the equilibrium state, when the material is unloaded, the arrangement of charges within the material lattice is such that the unit cell is uncharged, Fig 1A. However, when the material is mechanically deformed, there will be a charge redistribution within the unit cell. This redistribution will induce net charges on the faces of the unit cell and give rise to a net dipole moment, Fig 1B and 1C.
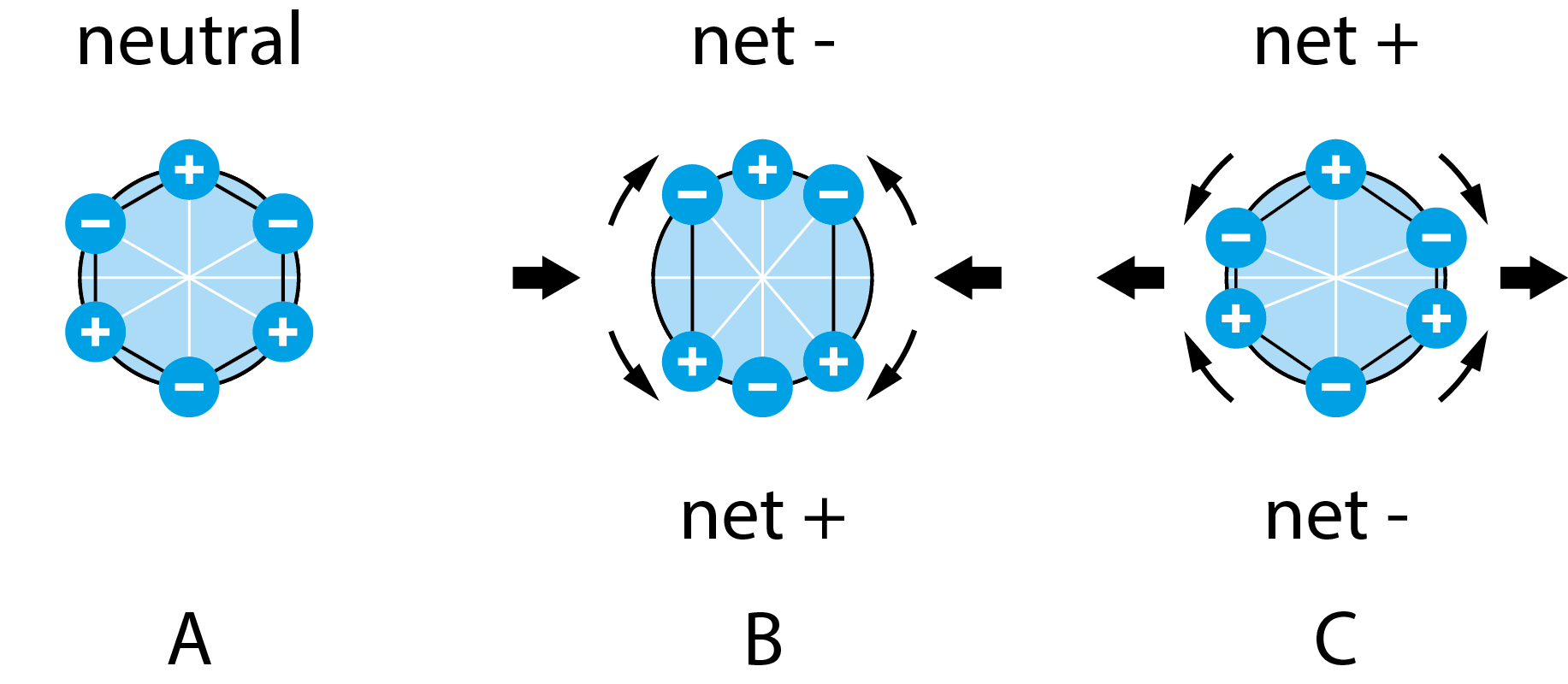
Figure 1. A schematic illustration of how piezoelectricity works. A) in equilibrium, the charges of the unit cell are distributed in such a way that there is no net dipole moment. B) When compressed, a net dipole moment arises in the vertical direction. C) when stretched, a net dipole moment arises in the horizontal direction.
The sum of the net charge contribution from all the unit cells will be an electrical polarization of the piece of material. This means that the applied mechanical force has induced a voltage over the material. For the polarization to happen, however, there must not be a symmetry center, Fig 2. As already mentioned, this requirement is only fulfilled by some materials. Until recently, the phenomenon had only been observed in solid-phase materials, but in early 2023, a pair of scientists reported observing the direct piezoelectric effect in ionic liquids.1
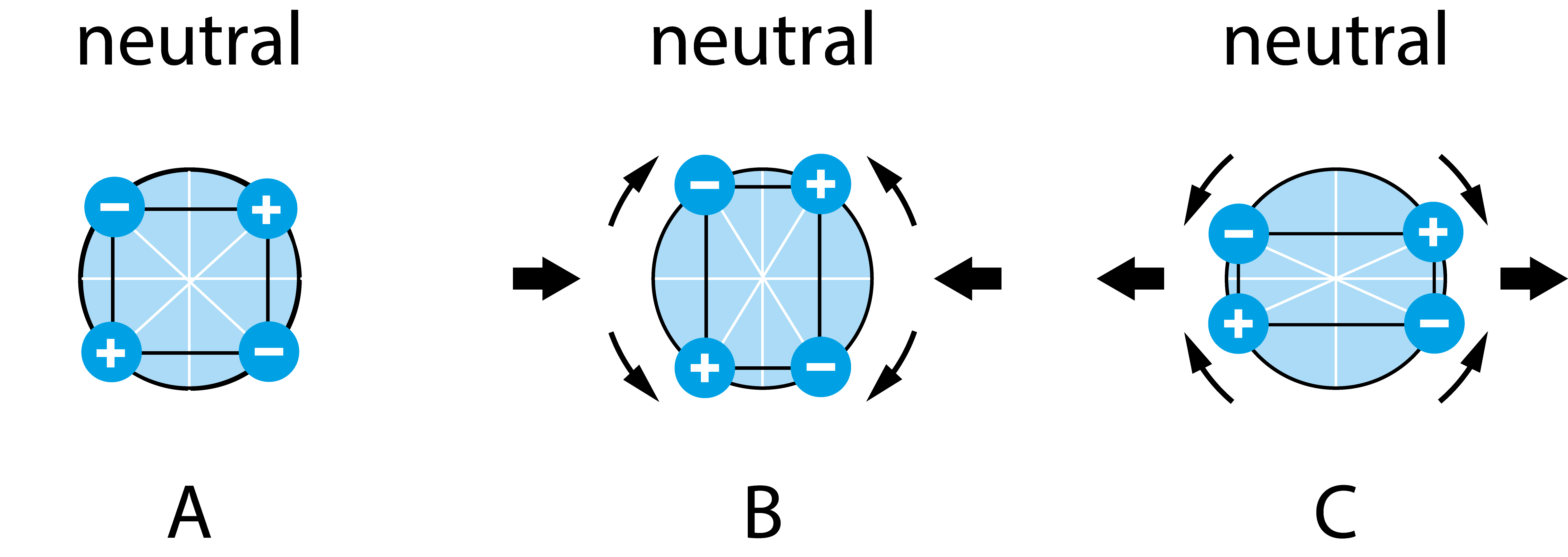
Figure 2. A schematic illustration of the charge distribution in the unit cell of a material with a symmetry center. Both in the equilibrium state (A), and when mechanically deformed (B, C), the charge distribution is such that a net dipole moment never arises.
The opposite phenomenon, i.e. where the material changes shape as a voltage is applied over its faces, is called the converse piezoelectric effect, and this was not discovered until a year later, in 1881.
Since the piezoelectric effect was discovered more than a century ago, it has spread into various applications and is now widely used. Areas include frequency control, in for example clocks, loudspeakers to generate sound, and microbalances, such as QCM and QCM-D, to monitor mass changes. But it doesn’t stop there. Now piezoelectricity is a candidate contributor to future sustainable energy supply. Light, wind, and thermal energy have long been obvious sources to use, and thanks to the piezoelectric effect, vibration has now been added to the list. One way to use vibrational sources for power generation is, for example, to harvest human kinetic energy via street or pavement tiles,2 i.e. to convert the energy of footsteps to electricity. Energy generated this way could be used to run for example streetlights or other low-voltage equipment in cities. In addition to energy harvesting, there are several applications in for example analytical chemistry where piezoelectric materials are used, including gas and liquid chromatography, virus detection, water determination, and trace metal analysis.3
Piezoelectricity is a property of certain materials that induces an electric current when mechanically stressed. It is used in, for example, frequency control and current generation applications.
Download the text as pdf below.
Malin graduated in engineering physics in 2006, where her research focused on the QCM-D technology. Since then, she has been scrutinizing the how’s and why’s of the world in general, and the world of QCM-D in particular.
