The fundamental resonance frequency of QCM-sensors is often 5MHz, but it could also be 10 MHz, 15MHz or even higher. So, what determines the value of the fundamental resonance frequency? Here we explain the theory behind the number.
Imagine a string with one end attached to a wall and the other one free. By introducing a motion to the free end, a wave is transmitted along the string impinging with the fixed end. At a certain frequency, a standing wave is formed. This is called the resonance frequency, f, and is correlated to the wavelength, λ, and the group velocity, υ, which in turn is a function of the density, rl, of the string and the string tension, F.
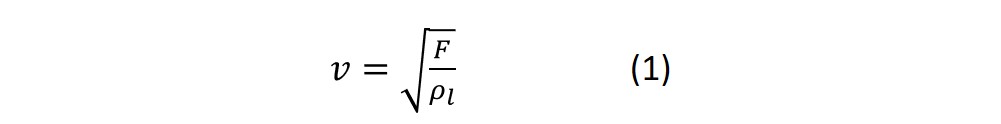
Here υ is the group velocity and rl the one-dimensional density.
The relation between the propagation speed of the wave, v, the wavelength, λ, and oscillation frequency, f, is
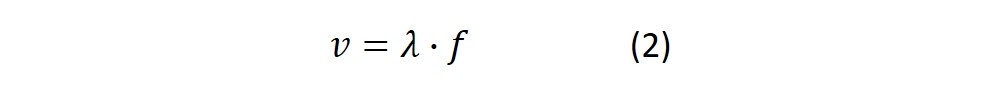
For the fundamental harmonic, the relation between frequency, f, and string length, L = λ/2, is from (1) and (2) as
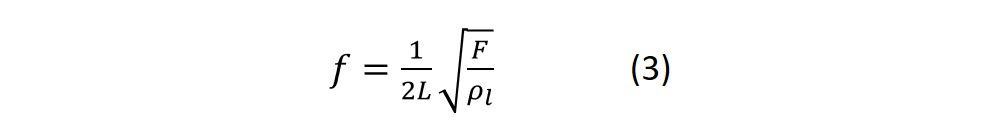
And for the n:th overtone, the relation is
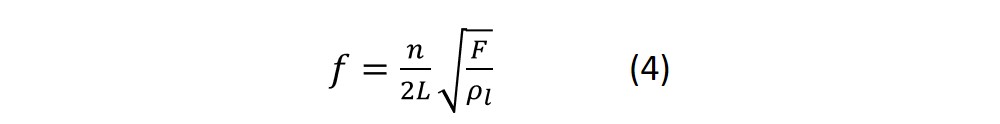
This means that the resonance frequency decreases if the length of the string increases, the density increases or the tension decreases.
If this is translated to an oscillating two- or three-dimensional material (such as a QCM sensor) one will see that the resonance frequency of the material is dependent on density, thickness and mass/pressure loading onto the sensor surface.
The speed of sound is given by
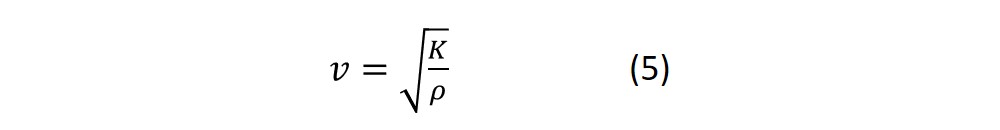where K is the bulk modulus (in case of a solid material) and ρ is the density.
The density for alpha quartz, which is a common material in QCM sensors, is 2648 kg/m3 and the bulk modulus is 37.5 GPa. This inserted in the equation above yields a propagation velocity of an acoustic wave of 3760 m/s.
A disk, such as a QCM sensor, of this material that is 340 micrometers thick will thus have a fundamental resonance frequency of
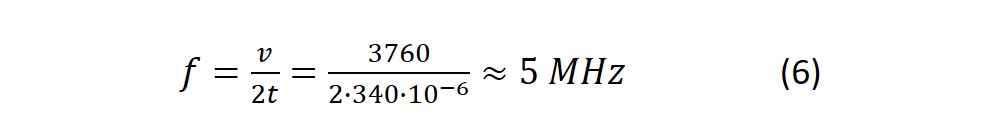Want to save the text for later? Download the text as pdf below
Why the QCM resonance frequency is 5MHz DownloadOverview
Gabriel Ohlsson, Ph.D., is a former employee at Biolin Scientific where he initially held a position as an application scientist and later as a sales manager. Dr. Ohlsson did his Ph.D. in engineering physics and has spent a lot of time developing sensing technologies for soft matter material applications. One of his main tools during this research has been the QCM-D technology.
